饲养管理

对于度量猪群规模的讨论，需参考一个地区的猪群(猪只)密度，或猪群内的饲养密度，因为猪群密度可能与猪群规模正相关。某些国家（如，丹麦）将较大猪群（和猪只）密度与较大猪群规模相混杂（Flori等，1995），进而阐述猪群规模效应。关于猪伪狂犬病，除考虑猪群规模为风险因素外，还需着重考虑区域内受感染的猪群或猪只密度，现今至少有五项研究证实这一观点（Austin等人，1993；Leontides等人，1994a，1995; Boelaert等，1999；Maes等，2000）。研究表明（Leontides等，1994b），将相关管理变量和猪群密度纳入统计模型后，猪群规模效应确实不再显著。

A discussion of herd size measures would be incomplete without reference either to herd (and pig) density in an area, which might also be positively correlated with herd size, or to pig stocking density within herds. Greater herd (and pig) density may be confounded with larger herd size at least in some countries, such as Denmark (Floriet al., 1995), and therefore might in part explain the reported herd-size effects. The importance of considering the density of infected herds or pig density on an area basis in addition to herd size as risk factors for pseudorabies was recognized in at least five studies (Austinet al., 1993; Leontideset al., 1994a, 1995; Boelaertet al., 1999; Maeset al., 2000). Indeed, in one study (Leontideset al., 1994b), the effect of larger herd size was no longer evident after related management variables and density of pigs had been included in the statistical models.

很少将大栏和空间的饲养密度作为引发猪病的风险因素进行研究，其原因有很多。首先，很难精确测量猪只密度，从分娩到育肥，数值会随着不同生产阶段发生改变。其次，即使存在较好的度量标准，也仅适用于大栏内，而度量猪群规模时，需要对群集或过度分散进行调整，所以研究分析会很复杂。再次，猪群规模与猪只密度之间存在共线性。在14篇有关胸膜炎或肺炎病变的研究中（表1：7位作者研究同时两种病变类型），只有7篇（50％）在度量猪群规模时对饲养密度进行测量，从而对控制猪群的肺炎问题提出标准建议（Done，1991年），强调最多改变20个环境变量，包括密度、空间和每栋猪舍内的猪数量。近期研究再次提出，对于育肥猪的呼吸道健康，空间和地面的饲养密度是重要的预测因素（Buddle等，1997；Stark等，1998；Maes等，2001）。

Pen and air-space stocking density have been investigated infrequently as risk factors for swine diseases, and there a number of possible reasons for this. First, pig density is difficult and tedious to measure accurately, and the value changes with the stage of production in farrow-to-finish herds. Secondly, even if a good measure exists, measurement is usually done at the pen level and herd-level analysis is complicated by the need to correct for clustering or over-dispersion. Thirdly, there is collinearity between herd size and pig density. Of the 14 unique reviewed studies of pleuritis or pneumonia lesions (Table 1: seven authors studied both lesion types), only seven (50%) evaluated a stocking density measure of herd size, yet standard recommendations for the control of pneumonia in problem herds (Done, 1991) emphasize alteration of up to 20 environmental variables, including density, air space, and pigs per building. The importance of air-space stocking density and floor-space stocking density as important predictors of respiratory health in finisher pig has been reaffirmed in recent studies (Buddleet al., 1997; Starket al., 1998; Maeset al., 2001).

另一项与地面、空间密度和猪群规模度量有关的因素也需考虑。多变量模型中，这些度量值可能存在共线性，这就使研究人员针对猪群规模得出一两个度量值后，便不再对其进行度量。实践中，通常采用最容易获取猪群规模的度量方式（例如，母猪数量或每年育肥猪出栏量），且无论选择哪种度量方式，作者均可以假设变量间的相关性足够高，能够相互代替。不过，后一种假设不一定正确。例如，笔者估算了三种常用的猪群规模度量方式之间的两两相关系数：作为全国养猪调查的一部分，调查了美国1306个分娩至育肥式猪场，统计其母猪数量、每年生猪销售量和总存栏量（美国农业部：动植物卫生检疫局：兽医处，1992年）。估算范围在0. 20至0.61，以此表明仅为中等线性关系。因此，多变量模型中，可采用多种猪群规模度量方法。

Another consideration relevant to the measurement of floor and air-space density and measures of herd size warrants comment. The possible collinearity of these measures in multivariable models may have dissuaded researchers from recording more than one or two measures of herd size. In practice, the most easily acquired measure of herd size (e. g. the number of breeding females or the number of finishers slaughtered per year) is generally used and, for whatever measure is selected, authors probably assume that the variables are sufficiently highly correlated to be interchangeable. The latter assumption may not necessarily be correct. For example, we estimated pairwise correlation coefficients between three frequently used measures of herd size: the number of breeding females, the number of pigs sold per year and the total inventory of pigs for 1306 US farrow-to-finish farms studied as part of the National Swine Survey (United States Department of Agriculture: Animal and Plant Health Inspection Service: Veterinary Services, 1992). The estimates ranged from 0. 20 to 0.61, which indicated only low to moderate linear relationships. Hence, multiple measures of herd size might be included in multivariable models.

猪群规模影响疾病产生的生物学原因

Biological reasons for an effect of herd size on disease occurrence

猪群规模增大，引入和传播病原的风险随之增加，以下会对其生物学原因进行论述。笔者注意到，通过管理手段（例如，生物安全措施、全进全出式生产及按日龄分群生产），也许能够降低大规模猪群所引发的风险，从而降低病原进入猪群或在猪群内部传播的风险。但是，美国一些小规模猪群所有者的管理方式风险较高，如与邻居交换公猪、参加集市和牲畜展览，以及在单一用途上更频繁地使用卡车，这样就削弱了小规模猪群的养殖优势。

In this section, we describe plausible biological reasons for increased risk of introduction and spread of infectious agents with increasing herd size. We note that large herds might be able to mitigate many of these increased risks by the use of management procedures (e.g. biosecurity practices, all-in, all-out production and age-segregated production) which decrease the risk of introduction of pathogens into herds or their within-herd transmission. In addition, owners of smaller herds in the USA frequently use riskier management practices, including swapping boars with neighbors, increased likelihood of attending fairs and livestock shows, and more frequent use of trucks for a single purpose, which counteract the benefits of small herd size.

猪群外部引入病原风险更大

Greater risk of introducing infectious agents form outside the herd

猪群规模增大，可能会增加猪群与外部潜在感染源直接和间接接触。如种猪与生长猪（20公斤左右）的引入、饲料和屠宰猪的运输以及人员出入。因此，若不针对上述事项采取防护措施，通常会增加引入病原的风险。以下，将更为详细地论述管理因素与猪群规模的相互关系（见猪群规模相关管理因素的影响）。

The number of direct and indirect contacts that a swine herd has with potential outside sources of infection may increase as the herds expand in size. These contacts include introduction of breeding and feeder pigs, transportation of feed and of slaughter animals and visitor. Consequently, unless protective management practices are used as outlined above, the risk of introduction of pathogens will also usually increase. We describe the interrelationships between management factors and herd size in more detail below (see Influence of management-related factors that are associated with herd size).

引入病原携带猪

Introduction of infectious agents with carrier pigs

为证实猪群规模效应，从外部购入后备母猪替换猪群中一定比例的母猪。假定后备母猪数量为n，源猪群中病原感染率为p，Marchevsky等（1989）认为由引种导致至少感染一头母猪的风险（P）服从二项分布。假设p= 0.01且在引种前未进行病原体检测，那么，一个500头母猪的猪群每年替换掉20%的母猪，其引入病原的风险(P)为0.64，同等替换率条件下，一个100头母猪的猪群，其风险(P)为0.18。新场启动时，从同一源猪群引种，同样会发生与猪群规模相关的类似现象。从理论上讲，大规模猪群所有者如果想要降低风险，可以从未感染猪群购买猪，或者只引入检测阴性的猪。

To demonstrate the effects of herd size, consider herds that replace a fixed proportion of the female breeding herd with gilts purchased from outside herds. Assuming a binomial distribution, Marchevskyet al.(1989) showed that the risk (P) of introducing at least 1 infectedfemale is wherenis the number of gilts introduced andpis the prevalence of the infectious agent in the source population. For example, assuming thatp= 0.01 and no testing for the agent was done prior to the introduction, then a herd of 500 sows replacing 20% of females per annum would have a risk (P) of 0.64 of introducing an infectious agent compared with a risk of 0.18 for a herd of 100 sows with the same replacement rate. A similar herd size-related phenomenon occurs when herds are initially established from the same source without mitigations. One possible strategy for owners of larger herds to mitigate this theoretically increased risk is to purchase pigs from non-infected herds or to only introduce test-negative pigs into their herds.

P=1-(1-p)^{n (1)}

Thorburn等人(1991)建议对公式1作出修正，使其包含未替换的样本，且可对公式进一步修正，即在感染率不同的猪群中对不同数量的猪进行抽样。以下不再赘述此类修正。另外，为与下一部分的模型进行直接比较，假设病原携带猪引入受感染猪群后，病原就会在该猪群内传播。

Thorburnet al.(1991) suggested a modification of equation 1 to include sampling without replacement, and the equation could be further modified to include sampling of variable numbers of pigs from herds with different prevalences of infection. For simplicity, we do not present these modifications here. Also, to allow direct comparison with the model in the following section, we assume that, once an infectious agent is introduced into a herd with an infected pig, it is transmitted to other pigs in the same herd.

空气传播引入病原

Introduction of infectious agents transmitted by airborne routes

实验数据表明，即使不引种或者限制与其他猪群接触，病毒性疾病通过空气传播引入病原同样会增加大型猪群的感染风险。如猪呼吸道冠状病毒（PRCV）和猪伪狂犬病毒（PRV）等传染病（据报道在丹麦发生过空气传播导致的传染病）在大规模猪群的感染风险明显增加（Henningsen等，1988；Christensen等，1990；Flori等，1995）。此外，这些研究发现，猪群规模的自然对数变换能够最优表述猪群规模对PRCV阳性或PRV阳性的单一影响。

Even for herds not introducing pigs and with limited contacts with other herds, there is empirical evidence that large swine herds are at increased risk of airborne introduction of viral diseases. For example, for infections such as PRCV and PRV (for which airborne transmission in Denmark has been reported), an increased risk of infection was evident in large herds (Henningsenet al., 1988; Christensenet al., 1990; Floriet al., 1995). In addition, the authors of these three studies found that a natural logarithmic transformation of herd size was the best formulation of the independent effect of herd size on the odds of positive PRCV or PRV status.

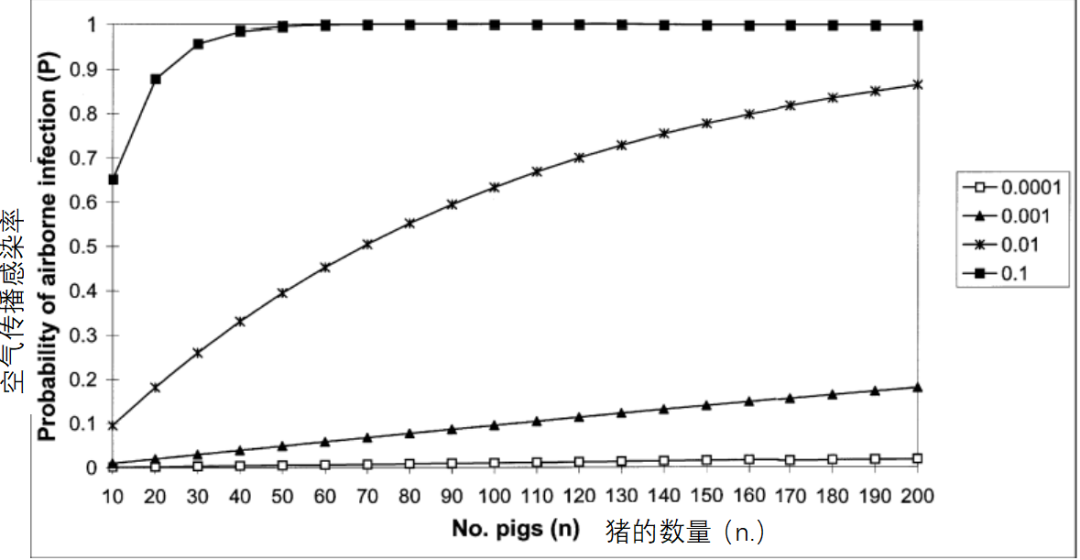
以实验为依据，假设猪群规模效应不再与猪群密度混杂，建议修正病原携带猪引入疾病的风险模型（公式1）中p和n的含义，从而将其应用于通过空气传播的病毒性疾病（Willeberg等，1994）。空气传播的情况下，P仍表示猪群被感染的概率，p指该猪群中单个猪只暴露于含有恒定病毒滴度（病毒数量/m^{3）的飞沫时被感染的概率，n是猪群暴露于病毒时的规模（Willeberg等，1994）。将猪群规模效应的意义概念化，可以认为猪群越大，占用的土地面积越大。假设每平方米占地面积的猪只密度固定，则500头规模育肥猪的占地面积是100头育肥猪所占面积的五倍。}

On the basis of this empirical evidence and the assumption that the herd-size effect was not confounded by herd density, we proposed that the model specified for the risk of disease introduction associated with carrier pigs (equation 1) could be applied to the airborne spread of viral diseases with modification of the meanings ofpandn( Willeberget al., 1994). In the context of airborne spread,Premains the probability of a herd becoming infected,pis the probability of an individual pig in the herd becoming infected if exposed to droplet nuclei containing virus of constant concentration (virus/m^{3) andnis the herd size at the time of exposure to the virus (Willeberget al., 1994). One way to conceptualize the meaning of the herd-size effect is to consider that larger herds occupy a greater area of land. For example, assuming a fixed density of pigs per m2of floor space, a herd of 500 fattening pigs would occupy an area five times greater than a herd of 100 fattening pigs.}

猪群被感染的概率（P）随着n和p非线性增加，但是当p足够小的时候，则是近似线性，即P= 1-(1-p)^{n≌np（如图1所示；p0.001时）。对于规模为n_{1和n2的两个猪群，每头猪感染风险为常数p，发生比（OR）为两个猪群受感染的比率，即OR = n1/ n2（上面提到的两个育肥猪群OR = 5）。在感染的ln(OR)对数模型中，存在对数转换。}}

The probability of the herd becoming infected (P) increases non-linearly withnandp, but whenpis small it can be shown that the relationship is approximately linear, i.e.P= 1-(1-p)^{n≌np (Fig.1; e.g. when p0.001). For two herds of sizen_{1andn2with constant riskpof infection on a per-pig basis, the odds ratio (OR) of becoming infected is the ratio of the two herd sizes, i.e. OR =n1/n2(OR = 5 for the two fattening herds referred to above). In a logistic model of the ln(OR) of infection, logarithmic transformation yields.}}

ln(OR)= ln(n_{1)- ln(n2)（2）}

现场数据用于逻辑回归分析，根据猪群规模变量（X）对ln(OR)进行建模，如下所示：

Field data are used in logistic regression analysis to model ln(OR) as a function of the herd-size variable(X) as follows:

In（OR）=X

=（x1-x2）（3）

对于猪群中的1个单元的变化，其中x1和x2是在连续测量下两个层面的猪群规模变量（X），是逻辑回归系数。笔者注意到等式2是等式3的特例，其中= 1且x1=ln(n1),x2= ln(n2)。

Wherex1andx2are two levels of the herd-size variable (X), measured on a continuous scale, and is the logistic regression coefficient for a 1-unit change in herd size. We note that equation 2 is a special case of equation 3 in which=1 andx1=ln(n1) andx2= ln(n2).

以下两项分析结果证明了此模型。Christensen等（1990年）分析了1987/88年丹麦南部爆发伪狂犬病的数据。案例猪群为伪狂犬病阳性猪群，未与其他感染猪群接触。对照组是与案例猪群相同地理区域的未感染猪群。分析中，HPU表示猪群规模，以反映猪的相对代谢规模。由于HPU的分布呈正偏态，因此采用HPU的对数变换模拟猪群规模效应。最终模型(针对猪群是否为一般猪群或SPF猪群，或者是育肥猪群或母猪群进行调整)包括ln (HPU)对的显著影响，约为1.26。随后一篇论文（Mousing等人，1991）中，对照样本仅限于11个邮区，这些地区可提供1987/88年和1989/90年猪群爆发流行病的完整数据。在此同样仅考虑育肥猪/母猪的管理，ln(HPU)的估算值为0.86。Leontides等（1994b）研究了德国北部母猪感染PRV的风险因素，通过控制由病原携带猪引发的感染（购买后备母猪或自繁自养），估算ln(猪群规模)的值为0.89。在一项关于猪群PRCV血清阳性的风险因素研究中，Flori等人（1995）对125个猪群进行数据分析，其中一个猪群与一个血清阳性猪群临近，此猪群感染PRCV的ln(HPU)估算值约为0.97。

Evidence in support of this simple model is provided by results of the following two analyses. Christensenet al.(1990) analysed data from outbreaks of pseudorabies in southern Denmark from 1987/88. Cases were pseudorabies-positive herds for which no known contact with other infected herds had occurred. Control herds were non-infected herds from the same general geographical area as the cases. In the analysis, herd size was expressed as HPU to reflect the relative metabolic sizes of the pigs. Because the distribution of HPU was positively skewed, a logarithmic transformation of HPU was used to model the effect of herd size. The final model (which adjusted for whether the herd was a conventional or SPF herd and whether the herd was a fattener or sow herd) included a statistically significant effect of ln(HPU) withestimated as 1.26.In a subsequent paper coauthored by one of us (Mousinget al., 1991), however, the control sample was restricted to 11 postal districts for which complete data were available for outbreak herds in both the 1987/88 and the 1989/90 epidemics. Here also, only fattener/sow management was accounted for, and theestimate for In(HPU) was 0.86. Leontideset al.(1994b) studied herd risk factors for PRV infection of breeding sows in northern Germany and estimatedfor ln(herd size) to be 0.89 after controlling for possible introduction of infection with carrier pigs (purchase of replacement gilts versus use of own inventory). In a study of risk factors for herd-level PRCV seropositivity, Floriet al.(1995) analysed data from a subset of 125 swine herds with a seropositive neighboring herd and found aln(HPU of own herd) estimate of 0.97 for PRCV infection.

图1.通过空气传播感染猪群的可能性（P=至少有1头猪被感染）与猪群中猪的数量（n）和单个猪只被感染的概率（p）的关系。基于文本中的等式1：P= 1-(1-p)n。

Fig. 1.Probability of airborne infection of swine herds (P= at least 1 pig becoming infected) as a function of the number of pigs in the herd (n) and the probability of an individual pig becoming infected (p). Calculations are based on equation 1 in the text:P= 1-(1-p)n.

对于可能发生于猪群间的空气传播，猜测预期数据与观测数据一致[即ln(HPU)的估算值接近1]，即病毒的空气传播遵循模型中固有假设：个体初次感染具有相同、独立的低风险特点。因此，如果该模型不适用或有误，或数据有其他偏差，的估算值则与1相差甚远。

For these examples of probable among-herd airborne transmission, we speculate that the agreement between observed and expected data [ i.e.estimates for In(HPU) close to 1] may be explained by the fact that airborne transmission of the virus closely follows assumptions inherent in the model: equal, independent and low risk of initial infection of individuals. In our opinion if the model were inappropriate or confounding or other biases were present in the data, then one would expect to findestimates substantially different from 1.

Manuel-Len和Casal（2001）还提出采用公式1对病毒通过空气传播的概率进行评估，从而说明1981/82年伪狂犬病在英国约克郡的猪群感染模式。

The use of equation 1 for a probabilistic assessment of virus airborne transmission has also been proposed by Manuel-Len and Casal (2001) to explain patterns of herd infection with pseudorabies in 1981/82 in Yorkshire, England.

下载畜牧堂APP了解更多